AzizKitten Package Guide

Installation

Provide instructions on how to install AzizKitten.

                pip install AzizKitten

Provide instructions on how to upgrade to a new version

                pip install --upgrade AzizKitten

Usage

mystery()

: This is a game with 3 diffrent levels. In each level you have to guess a number (or a number and a letter for the hard level) but you have a limit of attempts.

ment_calc()

: This is a game in math. You will get diffrent operations with numbers from 0 to 10 and you have 30 seconds to get the highest points possible.

sqrt(x)

: Return the square root of a number.

quad(a, b, c)

: Return the solutions of the quadratic equation (form of: ax² + bx + c = 0).

cubic(a, b, c, d)

: Return the solutions of the cubic equation (form of: ax³ + bx² + cx + d = 0).

quartic(a, b, c, d, e)

: Return the solutions of the quartic equation (form of: ax⁴ + bx³ + cx² + dx + e = 0).

quintic(a, b, c, d, e, f)

: Return the solutions of the quintic equation (form of ax⁵ + bx⁴ + cx³ + dx² + ex + f = 0).

bin_rep(n)

: Return the binary representation of a number n.

gcd(a, b)

: Return the GreatestCommonDivisor (PGCD) of two integers.

lcm(a, b)

: Return the LeastCommonMultiple (PPCM) of two integers.

factorial(x)

: Return the factorial of a number x ∉ ℤ^*_-

integrate(integrand, lower_limit, upper_limit)

: Return the result of the integral of 'integrand' from 'lower_limit' to 'upper_limit'.

exp(x)

: Return the exponential function of x.

log(x, base)

: Return the logarithm of a number with specific base (10 as default for decimal logarithm).

ln(x)

: Return the natural logarithm of a number (log_e).

floor(x)

: Return the floor of x, the largest integer less than or equal to x.

ceil(x)

: Return the ceiling of x, the smallest integer greater than or equal to x.

cbrt(x)

: Return the cubic root of x.

radians(x)

: Convert a value from the unit degrees to the unit radians.

degrees(x)

: Convert a value from the unit radians to the unit degrees.

derivative(func, value)

: Return the derivative of a function 'func' at a specific value.

is_prime(x)

: Return a True if x is prime number. Otherwise, it will return False

among_us(PlayersNumber, lang)

: This is a good game to play it with your friends or your family. And it is not the among us that you know. This is a little diffrent. Every Player take the phone and register his name. He has a chance to be a crewmate or an imposter. If he got crewmate he will get a word that each crewmate will get it. However, the imposter will not get it. After you register your name press enter to hide what you get and give the phone to the next player to register himself. Therefore, the first one that he registred himself start by saying a word related to the original one. Then next player say another word and so on... But the imposter doesn't know what is the word so he tries his best to know them what are they talking about and say a word. After some turns anyone can stop the game and start voting. Each one vote for what he want to kick and who gets the most vote he get out of the game. If he is the imposter so crewmates won. If not, the game continues until the importer get kicked or still only 2 players so the imposter won. NOTE: lang is the language of the word (ar for arabic / fr for french / eng for english (default)).

Examples

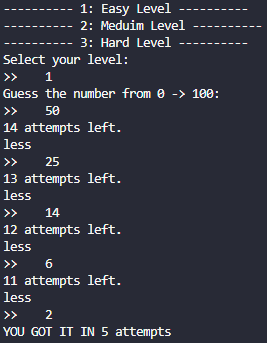
mystery()
Importing code:

                from AzizKitten import mystery
mystery()

OUTPUT:

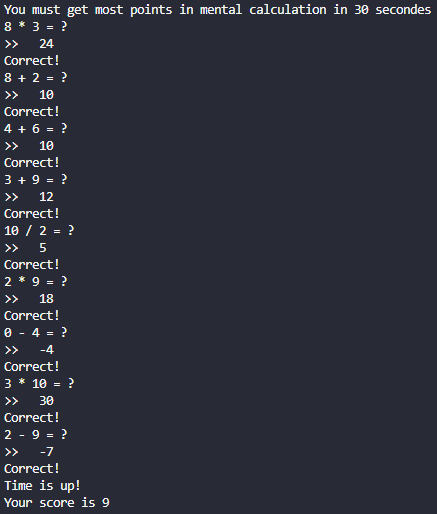
ment_calc()
Importing code:

                from AzizKitten import ment_calc
ment_calc()

OUTPUT:

sqrt(x)
Importing code:

                from AzizKitten import sqrt
x = sqrt(9) #x = 3.0
y = sqrt(-49) #y = 7j

quad(a, b, c) Online Solver
Importing code:

                from AzizKitten import quad
x = quad(-1, 1, 6)
print(x)
#OUTPUT: [-2.0, 3.0]
                quad(-1, -2, 3)
sol1 = quad.x1 #sol1 = 1
sol2 = quad.x2 #sol2 = -3.0

cubic(a, b, c, d) Online Solver
Importing code:

                from AzizKitten import cubic
x = cubic(1, -6, 11, -6)
print(x)
#OUTPUT: [1, 3.0, 2.0]
                cubic(1, 8, 19,12)
sol1 = cubic.x1 #sol1 = -1
sol2 = cubic.x2 #sol2 = -3.0
sol3 = cubic.x3 #sol3 = -4.0

quartic(a, b, c, d, e) Online Solver
Importing code:

                from AzizKitten import quartic
x = quartic(1, -9, 14, 36, -72)
print(x)
#OUTPUT: [6.00000000000062, 2.9999999999960343, 2.0000000000037175, -2.0000000000003713]
                quartic(1, -2, -5,10,-3)
sol1 = quartic.x1 #sol1 = 2.618033988749434
sol2 = quartic.x2 #sol2 = 1.3027756377335225
sol3 = quartic.x3 #sol3 = 0.3819660112488983
sol4 = quartic.x4 #sol4 = -2.3027756377318545

quintic(a, b, c, d, e, f) Online Solver
Importing code:

                from AzizKitten import quintic
x = quintic(1, 0, -52, 0, 576, 200)
print(x)
#OUTPUT: [-0.3511209248582378, 5.840287006067683, 4.320994337589649, -3.685009310616278, -6.125151108182818]
                quintic(1, 0, -11,0,21, 10)
sol1 = quintic.x1 #sol1 = 2.8080458514858657
sol2 = quintic.x2 #sol2 = 1.8761899147812595
sol3 = quintic.x3 #sol3 = -0.5706441578331696
sol4 = quintic.x4 #sol4 = -1.1059180033750788
sol5 = quintic.x5 #sol5 = -3.0076736050588764

bin_rep(n)
Importing code:

                from AzizKitten import bin_rep
x = bin_rep(0.1)
print(x)
OUTPUT:
0 01111111011 1001100110011001100110011001100110011001100110011010

If you want to get one of them you can just do like that:

                bin_rep(0.1)
Sign = bin_rep.sign #0
Exponent = bin_rep.exponent #01111111011
Mantissa = bin_rep.Mantissa #1001100110011001100110011001100110011001100110011010

You can use bin_rep.mantissa or bin_rep.fraction They are the same

gcd(a, b)
Importing code:

                from AzizKitten import gcd
x = gcd(15, 35)
print(x)
OUTPUT:
5

lcm(a, b)
Importing code:

                from AzizKitten import lcm
x = lcm(4, 2)
print(x)
OUTPUT:
4

factorial(n)
Importing code:

                from AzizKitten import factorial
x = factorial(5)
print(x)
y = factorial(1/2)
print(y)
OUTPUT:
120
0.8862127834776166

integrate(integrand, a, b)
Importing code:

                from AzizKitten import integrate
def integrand(x):
    return x**3 - 3*x**2 + 2*x
x = integrate(integrand, 0, 4)
print(x)
OUTPUT:
16.0

exp(x)
Importing code:

                from AzizKitten import exp
x = exp(1)
print(x)
OUTPUT:
2.718281828459045

log(x, base)
Importing code:

                from AzizKitten import log
x = log(100)
print(x)
OUTPUT:
2.0

The base is equal to 10 as default you can change it to another value if you want.

ln(x)
Importing code:

                from AzizKitten import ln
x = ln(2)
print(x)
OUTPUT:
0.6931471805599454

floor(x)
Importing code:

                from AzizKitten import floor
x = floor(-6.3)
print(x)
OUTPUT:
-7

ceil(x)
Importing code:

                from AzizKitten import ceil
x = ceil(1.2)
print(x)
OUTPUT:
2

cbrt(x)
Importing code:

                from AzizKitten import cbrt
x = cbrt(-27)
y = cbrt(8)
print(x)
print(y)
OUTPUT:
-3.0
2.0

radians(x)
Importing code:

                from AzizKitten import radians
x = radians(90)
print(x)
OUTPUT:
1.5707963267948966

degrees(x)
Importing code:

                from AzizKitten import degrees, pi
x = degrees(pi/4)
print(x)
OUTPUT:
45.0

derivative(func, value)
Importing code:

                from AzizKitten import derivative, pi
def f(x):
    return x**3
x = derivative(f, 2)
print(x)
OUTPUT:
12.000000992884452

is_prime(x)
Importing code:

                from AzizKitten import is_prime
x = is_prime(13)
print(x)
OUTPUT:
True

among_us(PlayersNumber, lang)
Importing code:

                from AzizKitten import among_us
among_us(5, "fr")

OUTPUT:

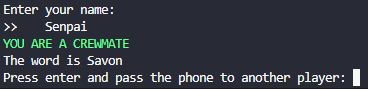
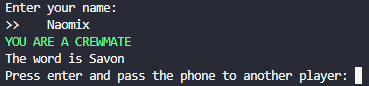
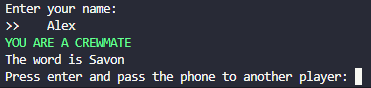
Then the game start.
Aziz: Clean
Senpai: bathroom
Dan: shower
and so on... Any player in any time can stops the game and start voting

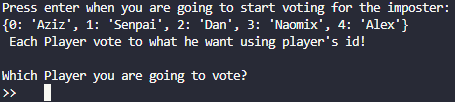
Btw voting by id not by the name. Let's suppose that most of the votes was on Naomix

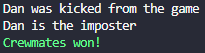
A crewmate was kicked from the game so we continue like we start, everytime each one say a word relateed to the original word... Let's suppose that Dan (the imposter) got most of the votes. Means crewmates are winners

Let's suppose that two players got the same amount of votes. Not both of them get kicked from the game. But, no one is eliminated and the game continues

Let's suppose that 3 players still in the game. And one of them got kicked and he is not an imposter. So the game still will only 2 players (an imposter and a crewmate). Therefore, The game is over and the imposter won

ChangeLog

version: 10.0.0

This is the first release for this Python package.
Release date: 19/12/2023
If you tracked any bug you can go to Bug Report

version: 10.1.0

What's New?

Added Binary Representaion function: bin_rep()
Added complex numbers for the root() function
Changed name for mental_calculation to ment_calc
Fixed a text shown in the output for ment_calc() function
Release date: 28/12/2023
If you tracked any bug you can go to Bug Report

version: 10.1.1 Hotfix

Fixed a problem in __init__.py file
Release date: 28/12/2023
If you tracked any bug you can go to Bug Report

version: 11.0.0 (Math update)

What's New?

Added the trigonometric functions (sin, cos, tan...)
Added common logarithm and natural logarithm
Added limits and integrals solver
Added exponential function (exp)
Added gcd (PGCD) and lcm (PPCM) calculator
Python 3.12 is now supported
Added some constants (pi, e, phi and gamma)
Release date: 08/02/2024
If you tracked any bug you can go to Bug Report

version: 11.1.0

What's new?

Added floor function
Added cubic equation solver
Removed root function for some reasons and added sqrt and cbrt functions instead
Added degrees and radians functions
Release date: 16/05/2024
If you tracked any bug you can go to Bug Report

version: 11.1.1 Hotfix

Fixed a mistake in cubic.py code
Release date: 16/05/2024
If you tracked any bug you can go to Bug Report

version: 11.1.2

Bug fixes
Release date: 20/05/2024
If you tracked any bug you can go to Bug Report

version: 11.1.3

Bug fixes
Release date: 21/05/2024
If you tracked any bug you can go to Bug Report

version: 11.2.0

What's new?

Added new function: quartic for solving quartic equations
Release date: 25/05/2024
If you tracked any bug you can go to Bug report

version: 11.3.1

Removed limit solving function
fixed an issue with factorial function
Release date: 30/05/2024
If you tracked any bug you can go to Bug report

version: 11.4.0

What's new?

Added derivative function
Release date: 04/06/2024
If you tracked any bug you can go to Bug report

version: 11.4.1 Hotfix

Fixed some issues
Release date: 04/06/2024
If you tracked any bug you can go to Bug report

version: 11.5.0

What's new?

Added quintic function to solve quintic equations
Added ceil function. (Return the ceiling of x, the smallest integer greater than or equal to x.)
Bug fixes with: logarithm functions (ln and log) and floor function
Added descriptions for every function in the library and the type of result that will return
Release date: 10/06/2024
If you tracked any bug you can go to Bug report

version: 11.6.1

What's new?

Added is_prime function
Bug fixes
Release date: 11/06/2024
If you tracked any bug you can go to Bug report

version: 11.6.3

Bug fixes: some functions takes more that 3 seconds to run
Release date: 12/06/2024
If you tracked any bug you can go to Bug report

version: 11.7.0

ln function now support complex numbers
Fixed a bug in trigonometric function with complex numbers
Release date: 13/06/2024
If you tracked any bug you can go to Bug report

version: 11.7.1

What's new?

Added tau constant
Added inf variable refers to infinity
Fixed a bug in sqrt function
Release date: 20/06/2024
If you tracked any bug you can go to Bug report

License

Copyright 2024 AzizKitten Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.